FLUIDA STATIK

“Hukum pascal menentukan tentang tekanan suatu titik”

PENGERTIAN HUKUM PASCAL

Bila ditinjau dari zat cair yang berada dalam suatu wadah, tekanan zat cair pada dasar wadah tentu saja lebih besar dari tekanan zat cair pada bagian di atasnya. Semakin ke bawah, semakin besar tekanan zat cair tersebut. Sebaliknya, semakin mendekati permukaan atas wadah, semakin kecil tekanan zat cair tersebut. Besarnya tekanan sebanding dengan pgh (p = massa jenis, g = percepatan gravitasi dan h = ketinggian/kedalaman)

Setiap titik pada kedalaman yang sama memiliki besar tekanan yang sama. Hal ini berlaku untuk semua zat cair dalam wadah apapun dan tidak bergantung pada bentuk wadah tersebut. Apabila ditambahkan tekanan luar misalnya dengan menekan permukaan zat cair tersebut, pertambahan tekanan dalam zat cair adalah sama di segala arah. Jadi, jika diberikan tekanan luar, setiap bagian zat cair mendapat jatah tekanan yang sama.

Contoh molekul fluida

Px = Py = Ps

Px yaitu tekanan yang tegak lurus dipermukaan ABFE

Py yaitu tekanan yang tegak lurus dipermukaan CDEF

Ps yaitu tekanan yang tegak lurus dipermukaan ABCD

            Tujuan dari gambar ini menunjukan tekanan fluida pada titik volume

1.      Mencari tekanan Px terhadap Ps

Pada tekanan Px memiliki luas permukan yaitu δ_z dan δ_y (m²) , dan

Pada tekanan Ps Sinϴ memilki luas permukaan yaitu δ_z dan δ_s (m²). Ditekanan Ps ada Sinϴ. Karena, Ps mempunyai kemiringan tertentu (ϴ = theta).

Mencari titik sin ϴ :

Dari gambar diatas kita bisa mendapatkan :

                                                               

Cara untuk memperoleh nilai-nilai tekanan adalah Hukum Newton 1 dengan Ʃ F= 0

Perhatikan uraian berikut :      P =  F/A  atau F = P. A

P = Pressure / Tekanan (Pa)

F = Force / Gaya (N)

A= Area / Luas Permukaan (m²)

·         Untuk membuktikan ∑ Fx = 0

Px.δy.δs – Ps.sinϴ. δs. δs = 0

Px.δy.δs = Ps.sinϴ δs. δs        { ( - ) dipindahkan ke kanan jadi ( + ) lalu δs dicoret }

     Px.δy = Ps.sinϴ δs             { δy = Ps.sinϴ δs , bisa dicoret }

Jadi : Px = Ps

·         Untuk membuktikan ∑ Fy = 0

Elemen fluida yang bekerja di sigma Fy = Px.area ABFE – Ps.cos ϴ. δs. δs – w

     = Px. δy.δs - Ps.sinϴ δs. δs

{ kenapa (-), karena Fy mendapatkan tekanan kebawah jadi nilainya (-) }

Jadi : ∑ Fy = 0

2.      Mencari tekanan Py terhadap Ps

Pada tekanan Py memiliki luas permukan yaitu δz dan δx (m²) , dan

Pada tekanan Ps Cosϴ memilki luas permukaan yaitu δzdan δs (m²).

Jadi, jawaban dari pertanyaan di atas adalah Tekanan di titik Px = Ps dan Py =  Ps_, Maka dapat kita simpulkan bahwa Px = Py = Ps  atau dengan kata lain tekanan di beberapa titik nilainya adalah sama besar .

Ø Persamaan Umum Variasi Tekanan Pada Sebuah Fluida Statik

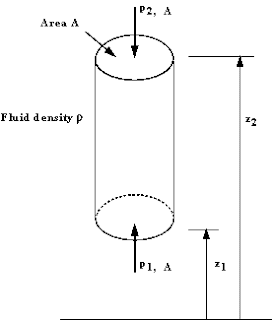
unsur silinder cairan dalam gambar diatas cenderung pada sudut ϴ vertikal panjang, penampang area A dalam cairan statis dari kepadatan massa density ρ . tekanan ketinggian z dan pada P +  δp dari ketinggian z + δz.

δp/δs = -ρg Cosϴ

Membuktikan ∑ Fs = 0

Elemen yang bekerja di sigma Fs :

PA – ( P + δp ) A – mg. Cosϴ = 0

PA ­– PA – δPA – mg. Cosϴ = 0                    ( kalikan volume / A )

 PA ­– PA – δPA – mg. Cosϴ = 0                   ( coret PA dan PA = 0 )

                – δPA – mg. Cosϴ = 0

                                 – δPA     = mg. Cosϴ

                                 – δPA     = ( ρ. v )g. Cosϴ

                                 – δPA     = ( ρ.A )g. Cosϴ         ( volume = A )

                                 – δPA     =  ρ.Aδs.g. Cosϴ        ( A kita coret )

                                    – δP     =  ρ.δs.g. Cosϴ

         – δP / δs =  ρ.g. Cosϴ                ( δs dijadikan untuk pembagi )

Jadi : δp/δs = -ρg Cosϴ

Variasi Tekanan Terhadap Ketinggian Pada Fluida Yang Dipengaruhi Gravitasi

Pada gambar diatas , kita bisa melihat unsur cairan yang kolom vertikal konstan cross sectional area A,  dikelilingi oleh cairan sama kepadatan massa density ρ. Fluida adalah beristirahat dan dalam kesetimbangan sehingga semua pasukan ke arah vertikal jumlah menjadi nol.

Didapat persamaan : P2 – P1 = -ρg ( z2 – z1 )

∑Fy = 0
elemen fluida yang bekerja pada sigma Fy :

P1A - P2A - mg = 0

                   P1A = P2A + mg

                   P1A = P2A + ρvg

                   P1A = P2A + ρA( z2 - z1 )g

                   P1A = A { P2 + ρ ( z2 - z1 )g }

                      P1 = P2 + ρ ( z2 - z1 )g

       - ρ(z2 - z1)g = P2 - P1

P2 – P1 = -ρg ( z2 – z1 )

Ø Kesamaan Besar Tekanan Fluida Statik Pada Dua Titik Dengan Ketinggian

Mempertimbangkan unsur silinder horizontal cairan pada gambar di diatas, dengan luas penampang A, dalam masa jenis ρ, tekanan P1 pada akhir tangan kiri dan tekanan P2 pada akhir tangan kanan.Cairan ini pada kesetimbangan sehingga jumlah gaya yang bekerja dalam arah x adalah nol.

jadi fluida yang bekerja di sigma Fx = PLA - PRA

jadi

∑fx = 0

PLA - PRA = 0

PLA = PRA                            ( A bisa dicoret  )

PL    = PR                               ( jadi tekanan dalam arah horizontal adalah konstan )

2 .Hasil ini adalah sama untuk setiap cairan terus menerus. Hal ini masih berlaku untuk dua tangki terhubung yang tampaknya tidak memiliki hubungan langsung, misalnya mempertimbangkan tangki pada gambar di atas :

          Pp = Pq + ρgh

          Pp = Pq + ρgz

Pp + ρgz = Pq + ρgz               ( ρgz bisa dicoret )

Jadi : Pp = Pq

semoga apa yang sudah saya paparkan bisa berguna untuk siapa pun :)